SORD

3D Support Operator Rupture Dynamics

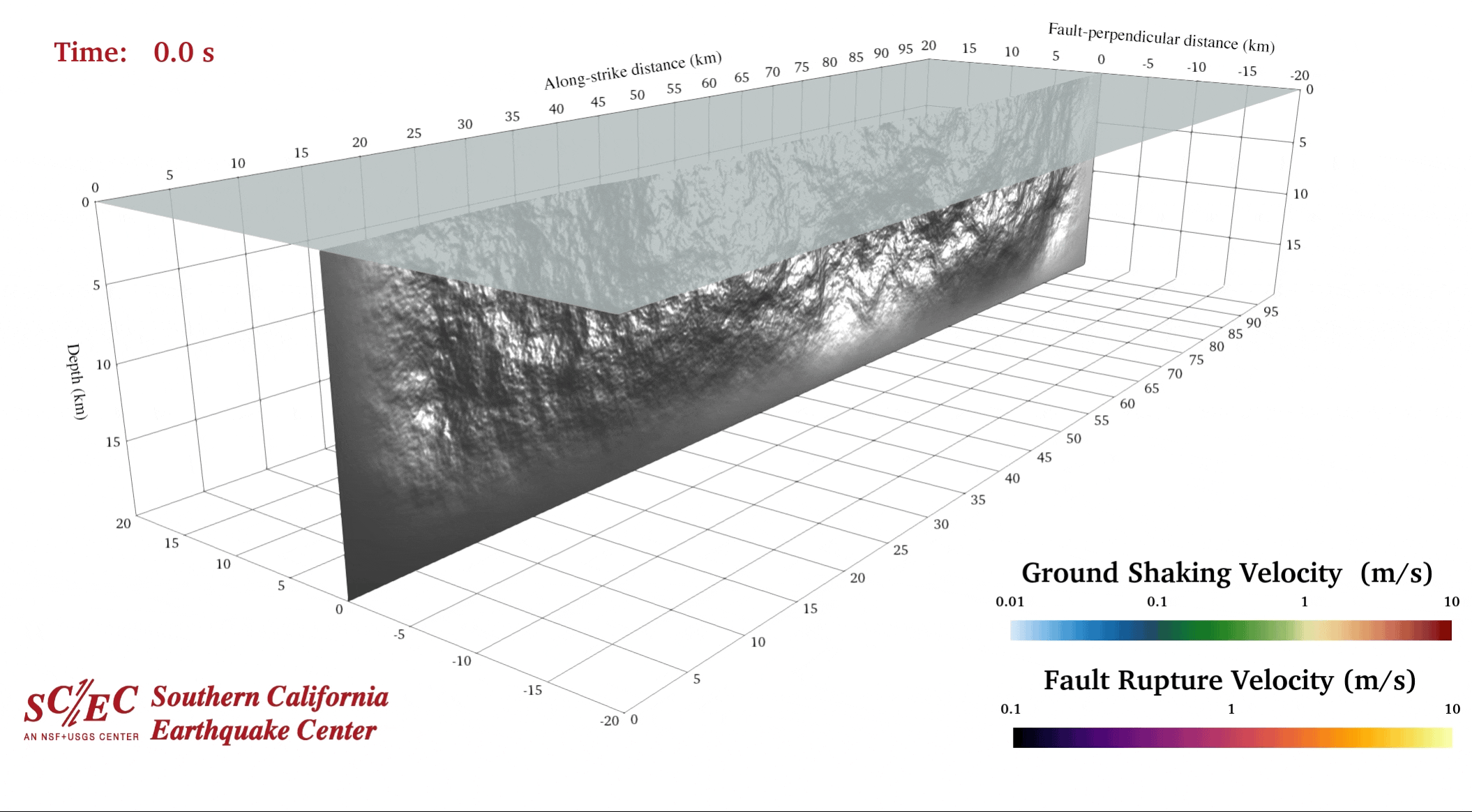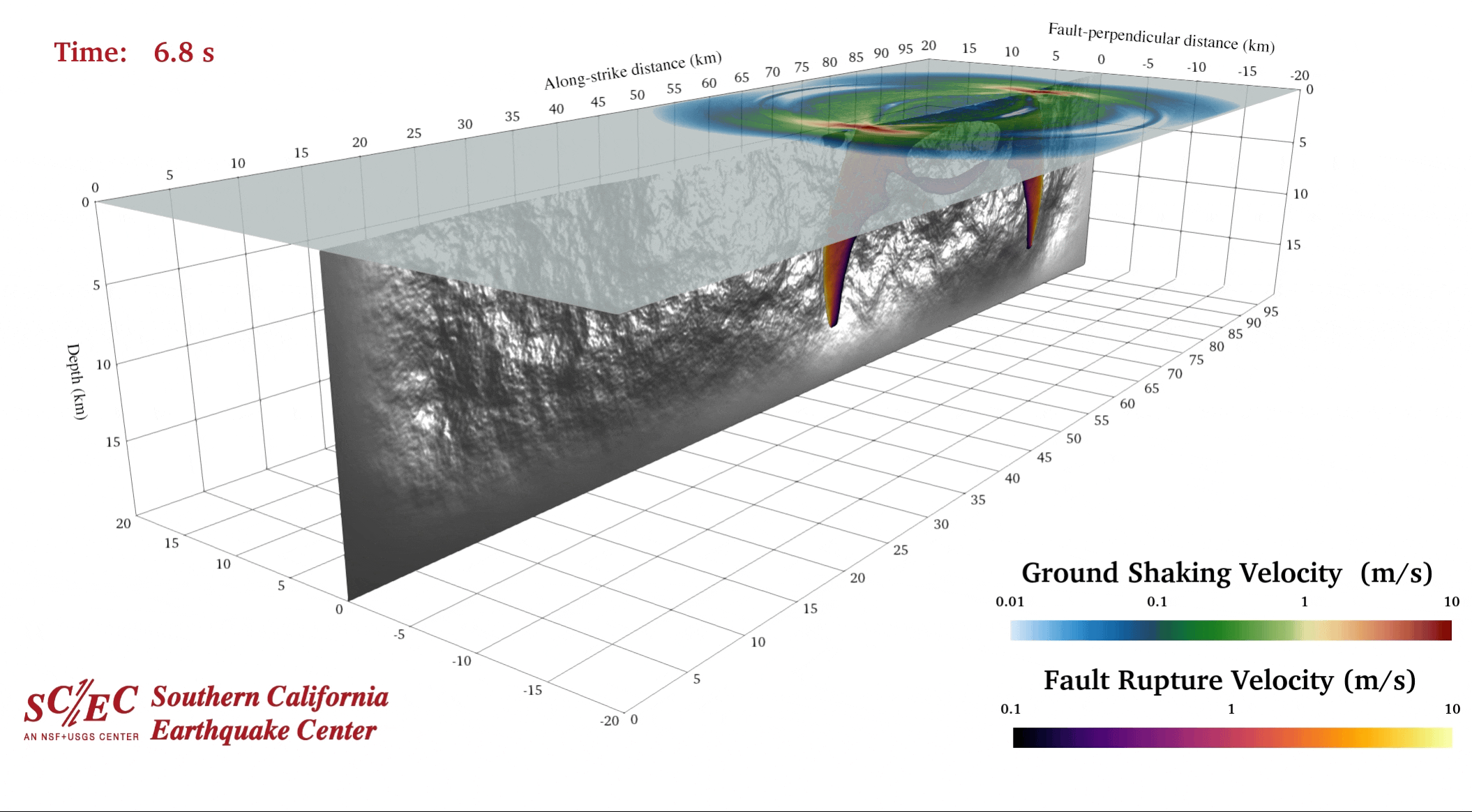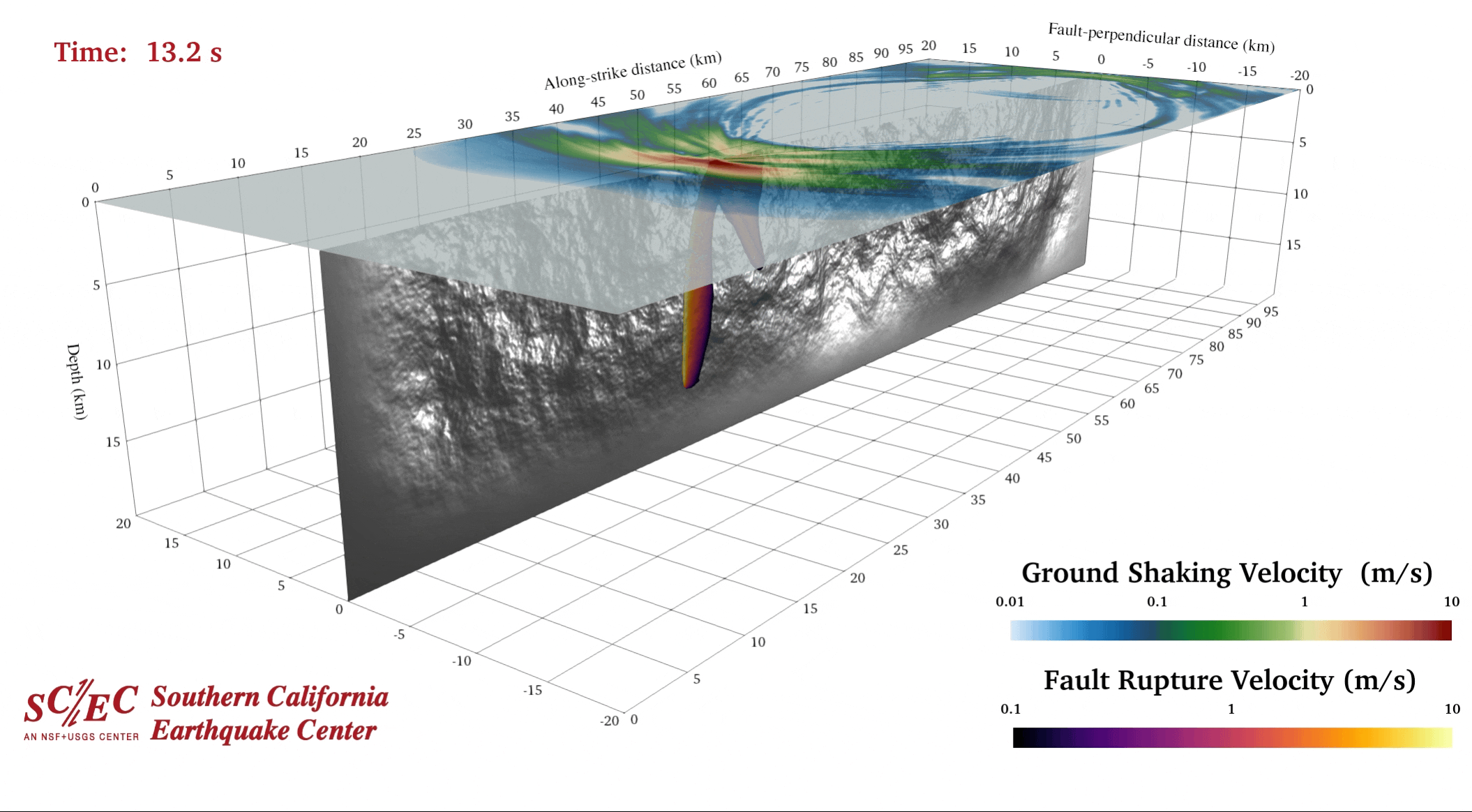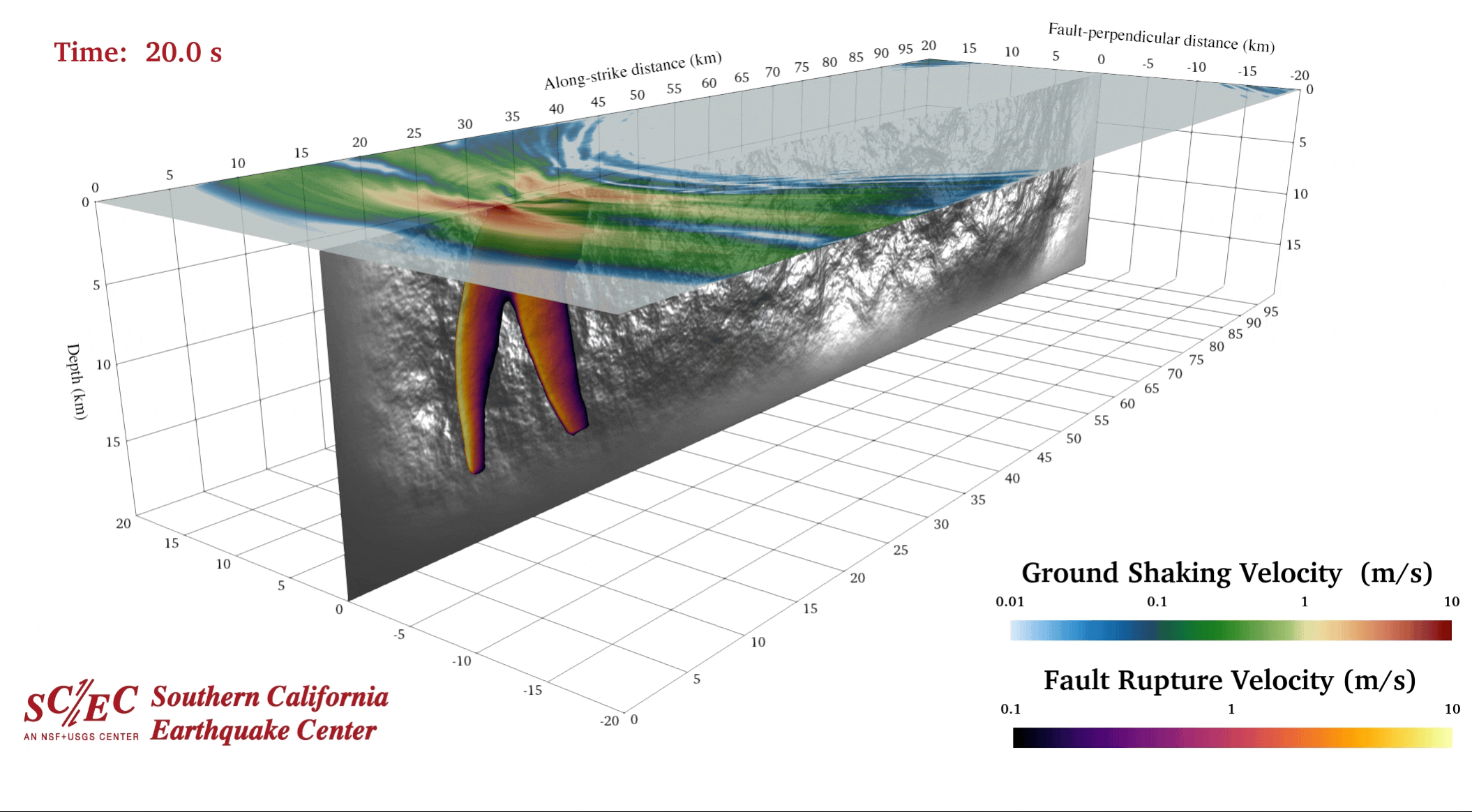
SORD latest version maintained by Yongfei Wang

Source code at here

Functional feature

Materials:

• Viscoelastic
• Plastoelastic
• Frequency-dependent Anelastic

Constitutive law

• Slip weakening
• Regularized rate and state
• Rate strengthening Slip weakening
• Thermal and porelastic response

Geometric structure

• Nonplanar fault
• Topographic effect
• Multiple-fault system

New branch

Since Zheqiang Shi, Brittany Erickson, Qian Yao , Willian Savran and Yongfei Wang joined Steven Day’s rupture dynamics group, a new branch of SORD has been developed. Currently, Yongfei Wang is the chief maintainer who uses it as a simulator of a physically plausible earthquake to study earthquake parameters and its evolution. The original Support Operator Rupture Dynamics (SORD) code simulates spontaneous rupture within a 3D isotropic viscoelastic solid. Wave motions are computed on a logically rectangular hexahedral mesh, using the generalized finite difference method of support operators. Stiffness and viscous hourglass corrections are employed to suppress suppress zero-energy grid oscillation modes. The fault surface is modeled by coupled double nodes, where the strength of the coupling is determined by a linear slip-weakening friction law. External boundaries may be reflective or absorbing, where absorbing boundaries are handled using the method of perfectly matched layers (PML). The hexahedral mesh can accommodate non-planar ruptures and surface topography SORD simulations are configured with Python scripts. Underlying computations are coded in Fortran 95 and parallelized for multi-processor execution using Message Passing Interface (MPI). The code is portable and tested with a variety of Fortran 95 compilers, MPI implementations, and operating systems (Linux, Mac OS X, IBM AIX, SUN Solaris). The source code is stored in Ely’s github

Maintainer Publications

1. Ely, G. P., Day, S. M., and Minster, J.-B. (2008), A support-operator method for viscoelastic wave modelling in 3-D heterogeneous media, Geophys. J. Int., 172(1), 331-344
2. Ely, G. P., Day, S. M., and Minster, J.-B. (2009), A support-operator method for 3-D rupture dynamics, Geophys. J. Int., 177(3), 1140-1150
3. Ely, G. P., Day, S. M., and Minster, J.-B. (2010), Dynamic Rupture Models for the Southern San Andreas Fault, Bull. Seismol. Soc. Am., 100(1), 131-150
4. Ben-Zion, Y., Rockwell, T. K., Shi, Z. Q., and Xu, S. Q. (2012), Reversed-polarity secondary deformation structures near fault stepovers, J. Appl. Mech., 79(3), 031025
5. Shi, Z. Q., and Day, S. M. (2013), Rupture dynamics and ground motion from 3-D rough-fault simulations, J. Geophys. Res., 118(3), 1122-1141
6. Wang, Y., and Day, S. M. (2017), Seismic source spectral properties of crack-like and pulse-like modes of dynamic rupture, J. Geophys. Res., 122(8), 6657-6684
7. Wang, Y., Day, S. M. and Denolle, M. A. (2018), Geometric Controls on Pulse-like Rupture in a Dynamic Model of the 2015 Gorkha Earthquake, J. Geophys. Res., 124(2), 1544–1568
8. Withers, K. B., K. B. Olsen, S. M. Day, and Z. Shi (2019), Ground Motion and Intraevent Variability from 3D Deterministic Broadband (0–7.5 Hz) Simulations along a Nonplanar Strike‐Slip Fault, Bull Seism Soc Am, 109(1), 229-250, doi:10.1785/0120180006
9. Withers, K. B., K. B. Olsen, Z. Shi, and S. M. Day (2019), Validation of Deterministic Broadband Ground Motion and Variability from Dynamic Rupture Simulations of Buried Thrust Earthquakes, Bull Seism Soc Am, 109(1), 212-228, doi:10.1785/0120180005
10. Wang, Y., and S. M. Day (2020), Effects of Off‐Fault Inelasticity on Near‐Fault Directivity Pulses, J. Geophys. Res., Solid Earth, 125(7), doi:10.1029/2019jb019074
11. Savran, W. H., and K. B. Olsen (2020), Kinematic Rupture Generator Based on 3‐D Spontaneous Rupture Simulations Along Geometrically Rough Faults, J. Geophys. Res., Solid Earth, 125(10), doi:10.1029/2020jb019464
12. Wang, Y., and G. A. Goulet(2021), Validation of fault displacements from dynamic rupture simulations against the observations from the 1992 Landers earthquake, Bulletin of the Seismological Society of America, Special Section: Fault Displacement and Near-Source Ground-Motion Models

Publications in which SORD is used

• Harris, R. A., et al. (2009), The SCEC/USGS dynamic earthquake rupture code verification exercise, Seismol. Res. Lett., 80(1), 119-126.
• Song, S. G., Dalguer, L. A., and Mai, P. M. (2013), Pseudo-dynamic source modelling with 1-point and 2-point statistics of earthquake source parameters, Geophys. J. Int., 196(3), 1770-1786
• Fan, W. Y., Shearer, P. M., and Gerstoft, P. (2014), Kinematic earthquake rupture inversion in the frequency domain, Geophys. J. Int., 199(2), 1138-1160
• Baumann, C., and Dalguer, L. A. (2014), Evaluating the compatibility of dynamic rupture-based synthetic ground motion with empirical ground-motion prediction equation, Bull. Seismol. Soc. Am., 104(2), 634-652
• Song, S. G. (2015), The effect of fracture energy on earthquake source correlation statistics, Bull. Seismol. Soc. Am., 105(2a), 1042-1048
• Vyas, J. C., Mai, P. M., and Galis, M. (2016), Distance and azimuthal dependence of ground-motion variability for unilateral strike-slip ruptures, Bull. Seismol. Soc. Am., 106(4), 1584-1599
• Mai, P., Galis, M., Thingbaijam, K., Vyas, J., and Dunham, E. (2017), Accounting for Fault Roughness in Pseudo-Dynamic Ground-Motion Simulations, Pure. Appl. Geophys., 174(9), 3419-3450
• Song, S. G., and Dalguer, L. A. (2017), Synthetic Source Inversion Tests with the Full Complexity of Earthquake Source Processes, Including Both Supershear Rupture and Slip Reactivation, Pure. Appl. Geophys., 174(9), 3393-3418
• Passone, L., and Mai, P. M. (2017), Kinematic Earthquake Ground-Motion Simulations on Listric Normal Faults, Bull. Seismol. Soc. Am., 107(6), 2980-2993
• Vyas, J. C., Mai, P. M., Galis, M., Dunham, E. M., and Imperatori, W. (2018), Mach wave properties in the presence of source and medium heterogeneity, Geophys. J. Int., 214(3), 2035-2052
• Harris, R. A., et al. (2018), A Suite of Exercises for Verifying Dynamic Earthquake Rupture Codes, Seismol. Res. Lett., 89(3), 1146-1162
• Dalguer, L. A., H. Wu, Y. Matsumoto, K. Irikura, T. Takahama, and M. Tonagi (2019), Development of Dynamic Asperity Models to Predict Surface Fault Displacement Caused by Earthquakes, Pure Appl Geophys, 10.1007/s00024-019-02255-8

Performance (strong and weak scaling)

23 single precision (four-byte) memory variables are required per mesh point. On current hardware, computation time is on the order of the one second per time step per one million mesh points. SORD scalability has been benchmarked up to 131 thousand processors at Theta (ALCF) and Fronteta (TACC).

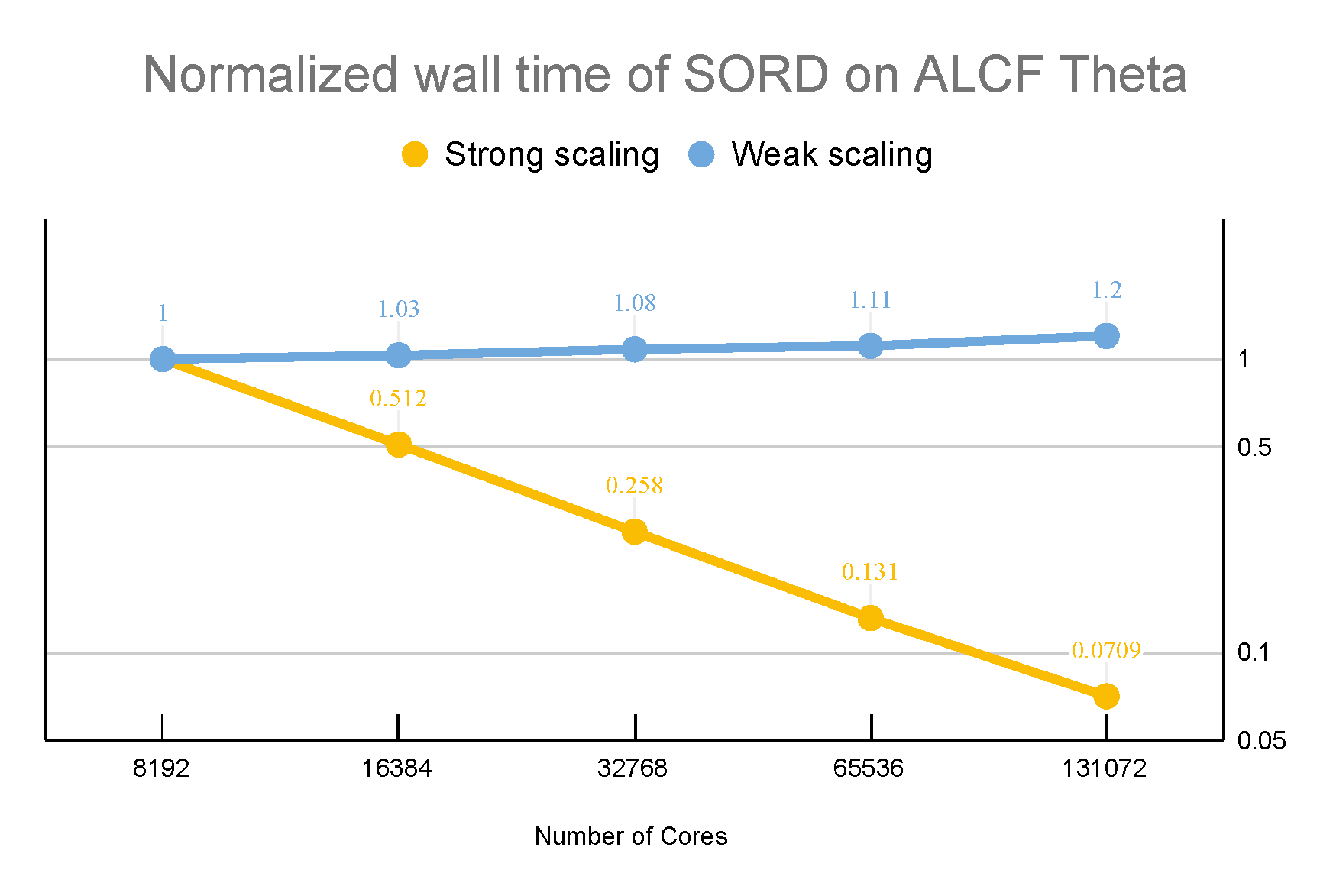
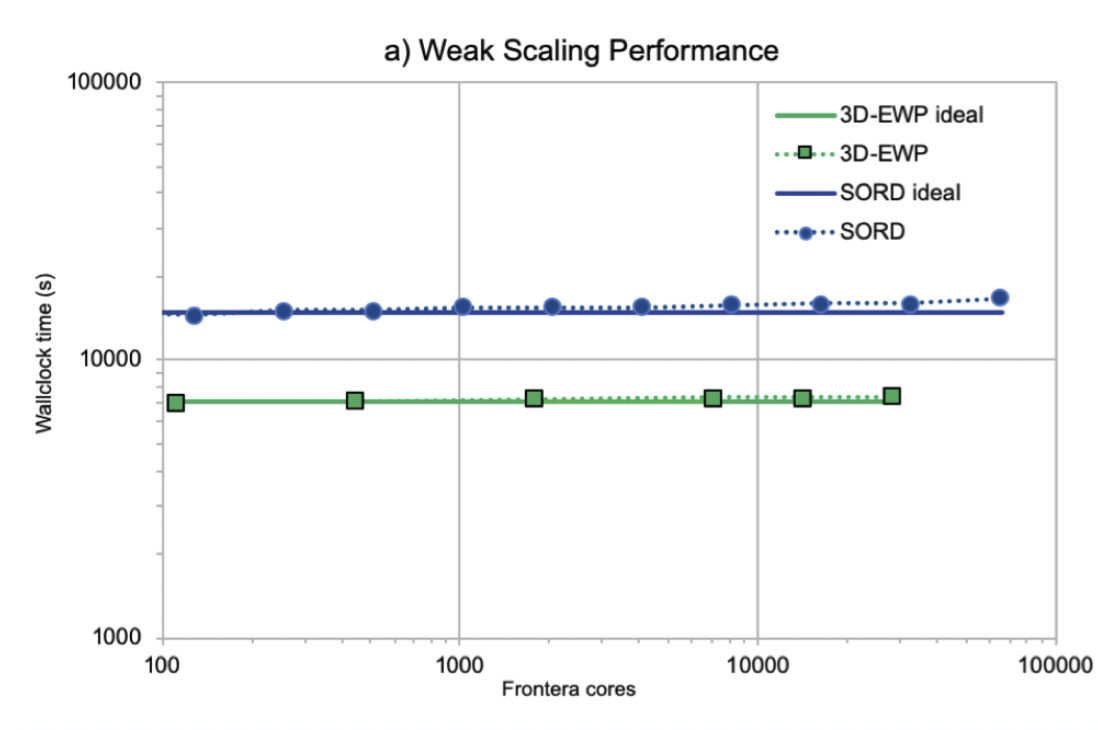
Simulation examples

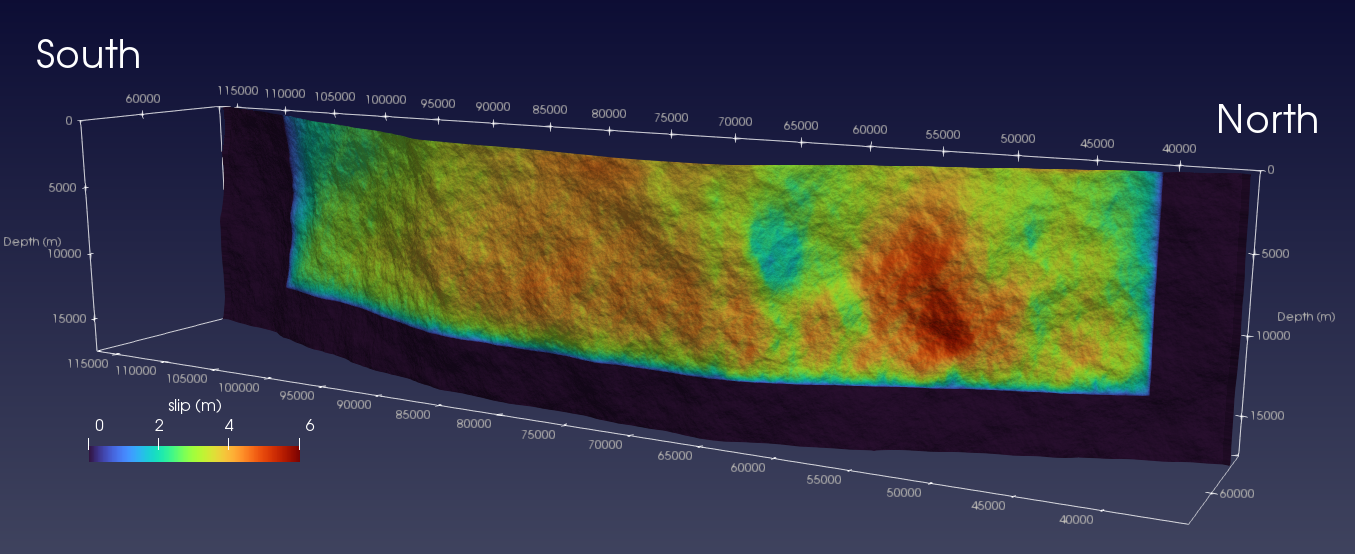
1992 Landers Earthquake Scenario

Fault roughness + off-fault plasticity

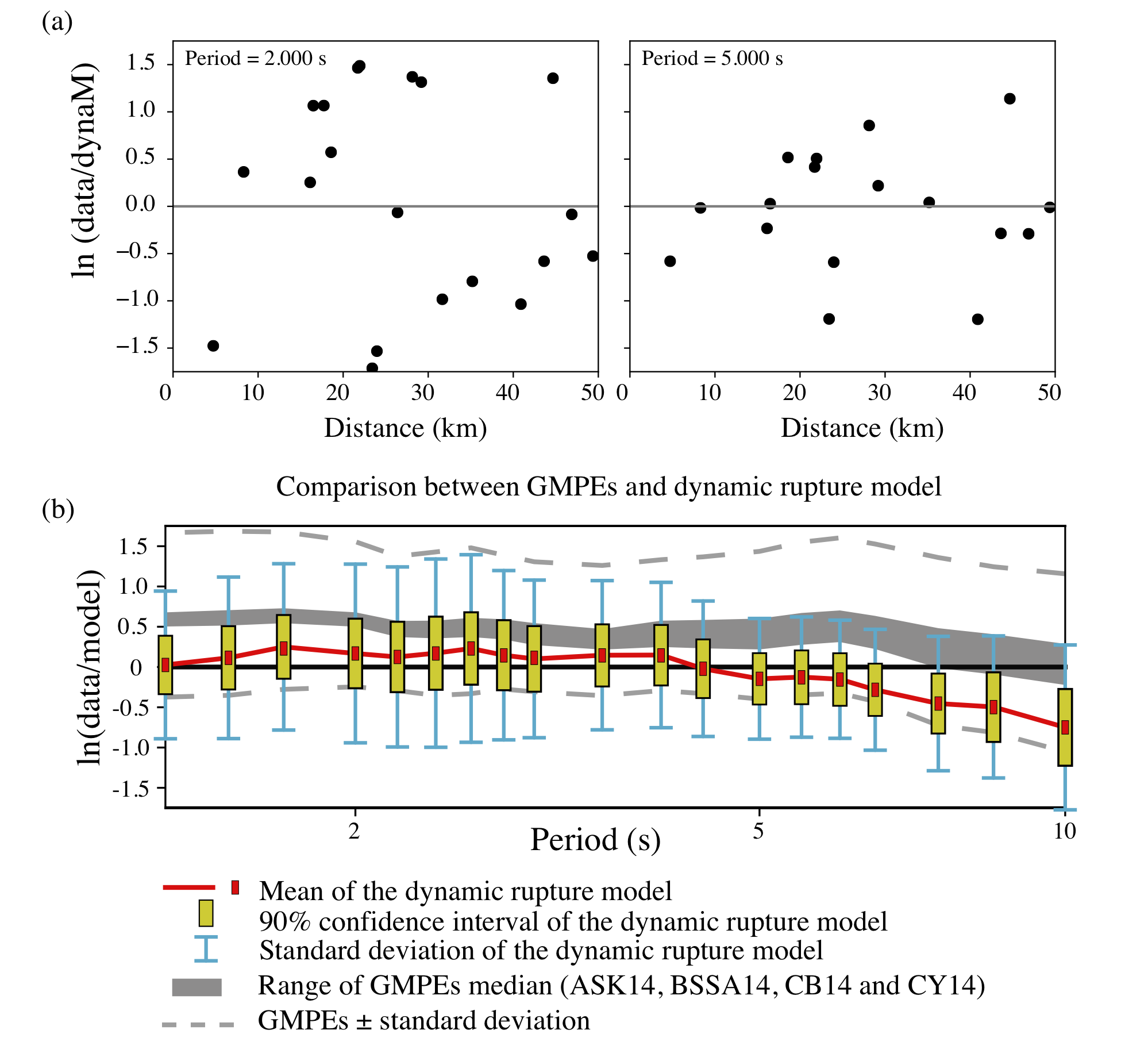
Ground-motion sanity check

Development logs

• Aug 21, 2018 Add frequency-dependent attenuation (to be checked by AWP benchmark)
• Aug 23, 2018 Add a function to exert a point source by setting strike, dip, rake and moment.

Bug found and fixed

• Bug in computing radiated energy, negative value (change temporal integral of fracture (+frictional) energy from rectangular to trapezoidal shape.)
• Bug in applying -R for reading initial stress tensor or bulk materials of cells (small variations after reading in) and may affect elastoplastic rupture dynamics
• Bug in PML zone when plasticity and rate and state law are applied. (Perhaps the rupture occures in PML zone)
• Bug found when in plasticity large stress drop are used ->(NAN wavefields). (will check from boundary or somewhere else)

legend

• means bug found
• means bug found has been fixed

If you found a bug in this program, you are so welcome to report it.